Scope terminators delimit the scope of some Procedure Division statements as described in Section 6.1.4.

The following are explicit scope terminators:

END-ACCEPT	END-ADD	END-CALL
END-COMPUTE	END-DELETE	END-DIVIDE
END-EVALUATE	END-IF	END-MULTIPLY
END-PERFORM	END-READ	END-RETURN
END-REWRITE	END-SEARCH	END-START
END-STRING	END-SUBTRACT	END-UNSTRING
END-WRITE

The following are implicit scope terminators:

• At the end of a sentence the separator period terminates the scope of all previously unterminated statements.
• In a statement containing another statement the next phrase of the containing statement after the end of the contained statement terminates the scope of all unterminated contained statements. Examples are ELSE and WHEN.

Whenever the term arithmetic expression appears in Procedure Division rules, it refers to one of the following:

• An identifier of a numeric elementary item
• A numeric literal
• A figurative constant ZERO (ZEROS, ZEROES)
• Two or more of the above separated by arithmetic operators
• Two or more arithmetic expressions separated by arithmetic operators
• An arithmetic expression enclosed in parentheses

A unary operator (a sign) can precede any arithmetic expression.

The identifiers and literals in an arithmetic expression must represent either of the following:

• Numeric elementary items
• Numeric literals on which arithmetic can be performed

Evaluation rules for arithmetic expressions depend on whether the mode of arithmetic in effect is native or standard.

6.4.1 Arithmetic Operators

Arithmetic expressions can use five binary and two unary arithmetic operators. A space must precede each operator and follow each binary operator.

The operators are as follows:

Binary Arithmetic Operator	Meaning
+	Addition
-	Subtraction
*	Multiplication
/	Division
**	Exponentiation
Unary Arithmetic Operator	Meaning
+	The effect of multiplication by +1
-	The effect of multiplication by -1

6.4.2 Formation and Evaluation of Arithmetic Expressions

The following rules apply regardless of the mode of arithmetic that is in effect.

Parentheses can be used to specify the order in which elements in an arithmetic expression are evaluated. Expressions within parentheses are evaluated first. If you nest sets of parentheses, evaluation starts with the innermost set of parentheses and proceeds to the outermost set.

If the arithmetic expression contains no parentheses, the compiler evaluates arithmetic operators in the following hierarchical order:

First	Unary plus and minus
Second	Exponentiation
Third	Multiplication and division
Fourth	Addition and subtraction

This order also applies within a single set of parentheses.

If two or more operators are at the same hierarchical level, and parentheses do not specify the sequence of operations, evaluation proceeds from left to right.

Parentheses can eliminate ambiguities in logic when there are consecutive operations at the same hierarchical level, or change the normal hierarchical sequence of evaluation.

Consider the following expression:

(3 * ITEMA - 2) / ((4 + ITEMB) * -ITEMA - ITEMC ** 2)

The order of evaluation is as follows:

1. 4 + ITEMB
2. -ITEMA
3. 3 * ITEMA
4. (The results of step 3) - 2
5. ITEMC ** 2
6. (The results of step 1) * (the results of step 2)
7. (The results of step 6) - (the results of step 5)
8. (The results of step 4) / (the results of step 7)

Each left parenthesis in an arithmetic expression must have a matching right parenthesis, and each right parenthesis must have a matching left parenthesis.

If the first operator in an arithmetic expression is a unary operator, a left parenthesis (() must immediately precede it when the arithmetic expression immediately follows an identifier or another arithmetic expression. For example:

CALL "OTHERPROG" USING ITEMA (-ITEMB) ITEMC.

The following rules apply to the evaluation of exponentiation:

1. If the value of an expression to be raised to a power is zero, the exponent value must be greater than zero. Otherwise, the size error condition exists. (See Section 6.6.4.)
2. If the evaluation yields both a positive and negative real number, the positive number is the result.
3. If the evaluation yields no real number, the size error condition exists.

If the evaluation of the arithmetic expression results in an attempted division by zero, the size error condition exists.

When a statement with an arithmetic expression does not refer to a resultant identifier, the compiler stores the results of the arithmetic expression in an intermediate data item. (See Section 6.6.1.)

6.4.3 Standard Arithmetic

When a floating-point data item is an operand in an arithmetic expression or an arithmetic statement, the rules for evaluation are described in Section 6.4.4.1.¹

When standard arithmetic is in effect, the following rules apply:

1. Any operand of an arithmetic expression that is not already contained in a standard intermediate data item is converted into a standard intermediate data item.
2. The size error condition is raised if the value is too large or too small to be contained in a standard intermediate data item.

A standard intermediate data item is of the class numeric and the category numeric. It is the unique value zero or an abstract, signed, normalized decimal floating-point temporary data item.

A standard intermediate data item has the unique value of zero or a value whose magnitude is in the range 10**-100 through 10**99 - 10**67, that is, (.100 000 000 000 000 000 000 000 000 000 00E-99) through (.999 999 999 999 999 999 999 999 999 999 99E+99)² inclusive, with a precision of 32 decimal digits.

When the value of a standard intermediate data item is not zero, the fraction contains no digits to the left of the decimal point and contains a digit other than zero to the immediate right of the decimal point.

A standard intermediate data item is rounded to 31 digits in the situations listed below.

1. When a standard intermediate data item is compared.
2. When a standard intermediate data argument is the argument of a function and there is no equivalent arithmetic expression defined for the rules of the function, unless otherwise specified in the rules for a function or unless situation 1, above, applies.
3. When a standard intermediate data item is being moved to a resultant-identifier for which the ROUNDED phrase has not been specified. Rounding of a standard intermediate data item may cause the size error condition to be raised.³

When a standard intermediate data item is being moved to a resultant-identifier for which the ROUNDED phrase is specified, the number of digits to which rounding occurs is as specified in the ROUNDED phrase.

When arithmetic expressions using addition, subtraction, multiplication, division, exponentiation, unary plus, and unary minus are evaluated, the exact result is truncated to 32 significant digits, normalized, and stored in a standard intermediate data item.

6.4.4 Native Arithmetic

When a floating-point data item is an operand in an arithmetic expression or an arithmetic statement, the rules for evaluation are those described in Section 6.4.4.1.

When native arithmetic is in effect, the following rules apply:

1. If the result of an arithmetic expression can be represented without loss of significance in 38 decimal digits or less, then decimal or computational operations are used to evaluate the expression.
2. When it is possible for an expression to produce more than 38 decimal digits, an intermediate data item is selected based on the MATH_INTERMEDIATE qualifier.

The compiler assumes that all possible digit positions of a variable are significant.

6.4.4.1 FLOAT Arithmetic

A double-precision binary floating-point intermediate data item is selected when /MATH_INTERMEDIATE=FLOAT is specified. On OpenVMS Alpha this is a G_floating or T_floating data item; on Tru64 UNIX or Windows NT this is a T_floating data item. See the Alpha Architecture Reference Manual for more information on floating-point data types and operations.

A G_floating data item has a sign bit, an 11-bit binary exponent, and a normalized 53-bit fraction with the redundant most significant fraction bit not represented. The magnitude of a G_floating data item is in the approximate range 0.56 * 10**-308 through 0.9 * 10**308. The precision of a G_floating data item is approximately one part in 2**52, typically 15 decimal digits.

A T_floating data item has a sign bit, an 11-bit binary exponent, and a 52-bit fraction. Compaq COBOL generates code that uses the finite, normalized, floating-point range capabilities of T_floating. The magnitude of a T_floating data item is in the approximate range 2.2 * 10**-308 through 1.8 * 10**308. The precision of a T_floating data item is approximately one part in 2**52, typically 15 decimal digits.

When the destination of an arithmetic statement is a floating-point data item, normal rounding takes place.

When an arithmetic expression references a floating-point operand, floating-point operations are used to evaluate the expression, and the result is represented in a floating-point intermediate data item. Floating-point operations use normal rounding; implicit conversions to integer are chopped. Compaq COBOL provides support for finite (normalized) floating-point values only.

When arithmetic expressions using addition, subtraction, multiplication, division, exponentiation, unary plus, and unary minus are evaluated, the exact result is truncated to 53 significant bits, normalized, and stored in a floating-point intermediate data item.

6.4.4.2 CIT3 Arithmetic

A decimal floating-point intermediate data item is selected when the qualifier /MATH_INTERMEDIATE=CIT3 is specified.

A CIT3 intermediate data item has the unique value of zero or a value whose magnitude is in the range 10**-100 through 10**99 - 10**81, that is, (.100 000 000 000 000 000E-99) through (.999 999 999 999 999 999E+99)⁴ inclusive, with a precision of 18 decimal digits.

When a CIT3 intermediate data item is being moved to a resultant-identifier for which the ROUNDED phrase is specified, the number of digits to which rounding occurs is as specified in the ROUNDED phrase; when the ROUNDED phrase is not present, no rounding takes place.

When arithmetic expressions addition, subtraction, multiplication, division, exponentiation, unary plus, and unary minus are evaluated, the exact result is truncated to 18 significant digits, normalized, and stored in a CIT3 intermediate data item.

6.4.4.3 CIT4 Arithmetic

A decimal floating-point intermediate data item is selected when /MATH_INTERMEDIATE=CIT4 is specified.

A CIT4 intermediate data item has the unique value of zero or a value whose magnitude is in the range 10**-100 through 10**99 - 10**67, that is, (.100 000 000 000 000 000 000 000 000 000 00E-99) through (.999 999 999 999 999 999 999 999 999 999 99E+99)¹ inclusive, with a precision of 32 decimal digits.

Rounding rules for CIT4 arithmetic are the same as those described in Section 6.4.3.

When arithmetic expressions using addition, subtraction, multiplication, division, exponentiation, unary plus, and unary minus are evaluated, the exact result is truncated to 32 significant digits, normalized, and stored in a CIT4 intermediate data item.

6.5 Conditional Expressions

A conditional expression specifies a condition the program must evaluate to determine the path of program flow. If the condition is true, the program takes one path; if it is false, the program takes another path. The IF, EVALUATE, PERFORM UNTIL, PERFORM VARYING, and SEARCH statements use conditional expressions. Any statement that can contain another imperative statement can contain a conditional expression.

A conditional expression can be either a simple or a complex condition. The types of simple conditions are the relation, class, condition-name, switch-status, sign, and success/failure conditions. Complex conditions are formed by using logical operators (AND, OR, NOT) with simple conditions. You can enclose conditions within any number of paired parentheses. However, embedding conditions this way has no effect on whether they are considered simple or complex.

6.5.1 Relation Conditions

A relation condition states a relation between two operands. The program compares the operands to determine whether the stated relation is true or false. The first operand is called the condition's subject. The second operand is called its object. Either operand can be an identifier, a literal, or the value of an arithmetic expression. The set of words that specifies the type of comparison is called the relational operator.

The format for a relation condition is as follows:

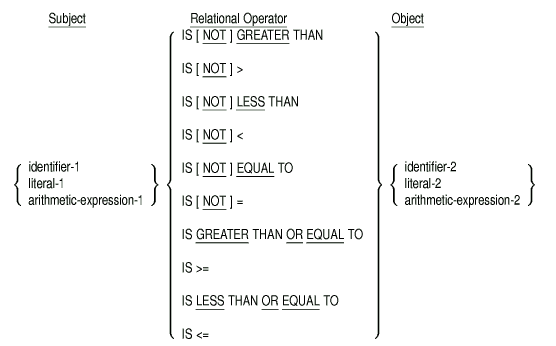
You can compare two numeric operands regardless of their USAGE. However, if one or both of the operands are not numeric, they must have the same USAGE. If either operand is a group item, then the comparison is treated as nonnumeric, since group items are always considered alphanumeric.

You must refer to at least one variable in a relation condition; you cannot refer only to literals.

A space must precede and follow each word in the relational operator. However, NOT and the key word or relation character that follows NOT are treated as a unit.

The following relational operators are equivalent:

• IS NOT GREATER THAN is equivalent to IS LESS THAN OR EQUAL TO
• IS NOT LESS THAN is equivalent to IS GREATER THAN OR EQUAL TO

Table 6-3 specifies valid true conditions that correspond to each relational operator.

Table 6-3 Relational Operators and Corresponding True Conditions

Relational Operator	True Condition
IS GREATER THAN IS > THAN	Subject is greater than object.
IS NOT GREATER THAN IS NOT > THAN	Subject is either less than or equal to object.
IS LESS THAN IS < THAN	Subject is less than object.
IS NOT LESS THAN IS NOT < THAN	Subject is either greater than or equal to object.
IS EQUAL TO IS = TO	Subject is equal to object.
IS NOT EQUAL TO IS NOT = TO	Subject is either greater than or less than object.
IS GREATER THAN OR EQUAL TO IS >=	Subject is greater than or equal to object.
IS LESS THAN OR EQUAL TO IS <=	Subject is less than or equal to object.

The following two sections specify the rules that apply to numeric and nonnumeric comparisons in relation conditions.

Comparison of Numeric Operands

When both operands are numeric, their algebraic values are compared. The program performs the necessary conversion if the data descriptions of the operands specify different USAGE. When you use operands that are literals or arithmetic expressions, their length (in terms of the number of digits represented) is not significant.

Unsigned numeric operands are assumed to be positive for comparison. A zero value is always treated the same way, whether or not the operand contains a sign.

Comparison of Nonnumeric Operands

When one (or both) of the operands is nonnumeric, each operand is considered a string of alphanumeric characters. Therefore, the operands are compared according to the program's collating sequence. (See the Section 4.1.2 paragraph in Chapter 4.)

If one of the operands is numeric, it must be either an integer literal or a data item described as an integer. The data item must be implicitly or explicitly described with USAGE DISPLAY. The treatment of the numeric data item is further affected by the following:

• If the nonnumeric operand is an elementary data item or a nonnumeric literal, the numeric data item is treated as though it were moved to an elementary alphanumeric data item of the same size. The content of this alphanumeric data item is then compared to the nonnumeric operand.
• If the nonnumeric operand is a group item, the numeric operand is treated as though it were moved to a group item of the same size. The content of this group item is then compared to the nonnumeric operand.
• When a numeric operand contains a sign, its sign is part of the string only if the other operand is a group item. Otherwise, the sign is removed and is not part of the comparison.

The two operands are compared character by character, beginning at the left end of each string. When the operation finds an unequal character pair, it uses that pair to evaluate the comparison. The greater operand is the one that contains the character with the higher collating sequence position. If the operands are of unequal size, the shorter operand is treated as if it were extended on the right with spaces to make it the same size as the other. Therefore, ABCD is greater than ABC (unless the program's collating sequence dictates otherwise).

Comparisons of Index-Names or Index Data Items

A program can compare the following:

• Two index-names
• One index-name and one literal or data item (other than an index data item)
• One index-name and one index data item
• Two index data items

The class condition tests whether the contents of an operand are numeric or alphabetic. It also determines if an alphabetic operand contains only uppercase characters, only lowercase characters, or if an operand is in conformance with class-name. The general format is as follows:

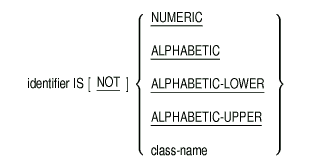
The identifier must reference a data item whose usage is explicitly or implicitly DISPLAY or COMP-3. If the identifier is a function-identifier, it must reference an alphanumeric function.

The following rules apply to the NUMERIC test:

1. The test is true when the operand contains only the characters 0 to 9 and the operational sign (subject to the next rule); otherwise, it is false.
2. The operand must contain an operational sign if its PICTURE clause specifies a sign. If the PICTURE clause does not specify a sign, the operand must not contain one. If the operand contains a sign that is not specified, or if a sign is specified and the operand does not contain one, the NUMERIC test is false.
3. You cannot use the test for an operand described as alphabetic or a group item containing signed elementary items.

The following rules apply to the ALPHABETIC test:

1. The test is true when the operand contains only the characters A to Z, a to z, and the space; otherwise, it is false.
2. You cannot use the ALPHABETIC test for an operand described as numeric.

The ALPHABETIC-LOWERCASE test is true when the operand contains only the characters a to z, and the space; otherwise, it is false.

The ALPHABETIC-UPPERCASE test is true when the operand contains only the characters A to Z, and the space; otherwise, it is false.

The class-name test is true when the operand consists entirely of the characters listed in the definition of class-name in the SPECIAL-NAMES paragraph. The class-name test must not be used with an item whose data description describes the item as numeric.

NOT and the key word following it are treated as a unit. For example, NOT NUMERIC is a test for determining that the operand is nonnumeric.